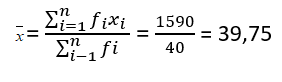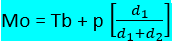Pengertian Mean, Median, & Modus serta Masing-Masing Contohnya

Mean

Mean atau rata-rata hitung adalah nilai yang diperoleh dari jumlah sekelompok data dibagi dengan banyaknya data. Rata-rata disimbolkan dengan x.

• Mean Data Tunggal

Keterangan:
ẋ = mean          
n = banyaknya data
x_i= nilai data ke-i

Contoh : Nilai UAS fisika mahasiswa kelas 2KB07 adalah 80, 70, 72, 86, 68, 78, 84, 66, 88, 92, 64, 78, 76, 84, 90. Tentukan nilai rata-ratanya….

Jawab   :

• Mean Data Bergolong

Keterangan:
x_i = nilai tengah data ke-i
f_i = frekuesni data ke -i

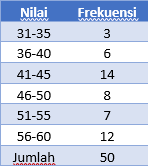
 Contoh : Tentukan rata-rata dari data berikut

Jawab : Cari  nilai xi dan fi dari masing-masing nilai :

Penyelesaian :

Median

Median adalah nilai data yang terletak di tengah setelah data diurutkan. Dengan demikian, median membagi data menjadi dua bagian yang sama besar. Median (nilai tengah) disimbolkan dengan Me.

• Median Data Tunggal

Jika banyak data ganjil maka Me adalah data yang terletak tepat yang ditengah setelah diurutkan.  Jika banyak data genap maka Me adalah ratarata dari dua data yang terletak di tengah setelah diurutkan.

Contoh :

Tentukan median dari data berikut : 3,7,2,8,6,9,1,5,4,2,3

Jawab : Data diurutkan : 1,2,2,3,3,4,5,6,7,8,9. Karena banyak data berjumlah ganjil maka letak median ada pada data ke-6 yaitu 4

Tentukan median dari data berikut : 6,8,3,5,9,1,3,2,5,4,7,8

Jawab : Data diurutkan : 1,2,3,3,4,5,5,6,7,8,8,9. Karena banyak data berjumlah genap maka letak median ada pada data ke 6 & 7 dan di rata-rata yaitu (5+5)/2 = 5

• Median Data Bergolong

Keterangan:
Me = median
Tb = tepi bawah kelas median
p = panjang kelas
n = banyak data
F = frekuensi kumulatif sebelum kelas median
f = frekuensi kelas median

Contoh : Tentukan median dari data berikut

Jawab : Cari nilai F (frekuensi kumulatif) dari masing-masing nilai :

Penyelesaian :

Modus

Modus adalah data yang paling sering muncul atau memiliki frekuensi tertinggi. Modus dilambnagnkan dengan Mo.

• Modus Data Tunggal

Modus dari data tunggal adalah data yang paling sering muncul.

Contoh : Tentukan modus dari data berikut : 2,5,7,6,9,1,2,5,4,6,7,8,4,3,5,2,3,4,5,6,9,9      

Jawab : Data diurutkan : 1,2,2,2,3,3,4,4,4,5,5,5,5,6,6,6,7,7,8,9,9. Modus dari data tersebut yaitu 5 karena muncul sebanyak 4 kali

• Modus Data Bergolong

Keterangan :
Mo : modus
Tb : tepi bawah kelas modus
p : panjang kelas
d₁ : selisih frekuensi kelas modus dengan kelas sebelumnya
d₂ : selisih frekuensi kelas modus dengan kelas sesudahnya

Contoh : Tentukan modus dari data berikut :

Jawab : Kelas dengan frekuensi terbanyak 15 maka modus terletak diantara kelas 61-70;

tb = 51-0,5 = 50,5

p = 10 (41-50)

d₁ = 15-6 = 9

d_{2 = 15-11 = 4}